--题外图

【基础知识精讲】

1.正弦定理、三角形面积公式

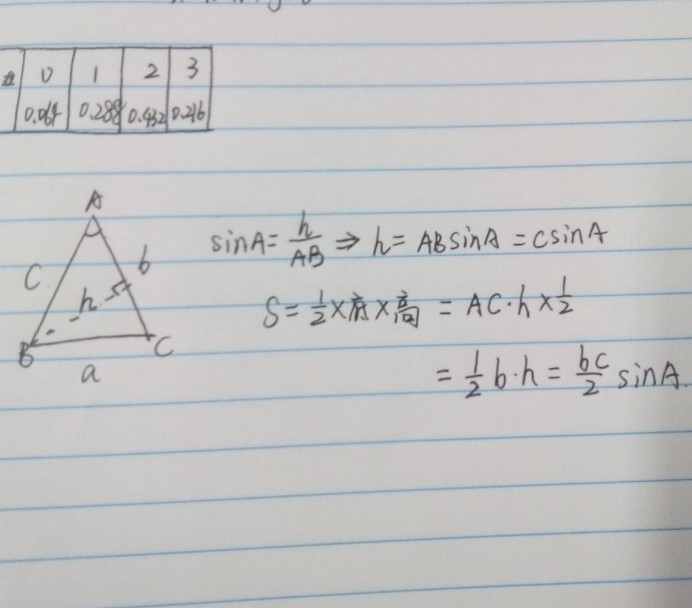
正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，并且都等于该三角形外接圆的直径，即：===2R.

面积公式：S△=bcsinA=absinC=acsinB.

2.正弦定理的变形及应用

变形：(1)a=2RsinA,b=2RsinB,c=2RsinC

(2)sinA∶sinB∶sinC=a∶b∶c

(3)sinA=,sinB=,sinC=.

应用(1)利用正弦定理和三角形内角和定理，可以解决以下两类解斜三角形问题：

a.已知两角和任一边，求其他两边和一角.

b.已知两边和其中一边的对角，求另一边的对角.

一般地，已知两边和其中一边的对角解三角形，有两解、一解、无解三种情况.

①A为锐角时

②A为直角或钝角时.

(2)正弦定理，可以用来判断三角形的形状.其主要功能是实现三角形中边角关系转化.例如：在判断三角形形状时，经常把a、b、c分别用2RsinA、2RsinB、2RsinC来代替.

3.余弦定理

在△ABC中，有a2=b2+c2-2bccosA;

b2=c2+a2-2accosB；

c2=a2+b2-2abcosC；

变形公式：

cosA=,cosB=,cosC=

在三角形中，我们把三条边(a、b、c)和三个内角(A、B、C)称为六个基本元素，只要已知其中的三个元素(至少一个是边)，便可以求出其余的三个未知元素(可能有两解、一解、无解)，这个过程叫做解三角形，余弦定理的主要作用是解斜三角形.

4.解三角形问题时，须注意的三角关系式：A+B+C=π

0＜A，B，C＜π

sin=sin=cos

sin(A+B)=sinC

特别地，在锐角三角形中，sinA＜cosB,sinB＜cosC,sinC＜cosA.

 

【重点难点解析】

掌握正、余弦定理，并学会用其余弦定理解三角形.

例1  在△ABC中，已知A＞B＞C，且A=2C,b=4,a+c=8，求a、c的长.

解：由正弦定理=及A=2C得=,即=,

∴cosC=.

由已知a+c=8=2b及余弦定理，得

cosC==

==.

∴=，整理得(2a-3c)(a-c)=0

∴a≠c,∴2a=3c.

∵a+c=8,∴a=,c=.

例2  在△ABC中，如果lga-lgc=lgsinB=-lg，且B为锐角，试判断此三角形的形状.

解：∵lga-lgc=lgsinB=-lg,

∴sinB=

又∵0°＜B＜90°，∴B=45°

由lga-lgc=-lg,得= .

由正弦定理得= .

即2sin(135°-C)= sinC

即2［sin135°cosC-cos135°sinC］=sinC.

∴cosC=0,得C=90°

又∵A=45°,∴B=45°

从而△ABC是等腰直角三角形.

例3  如图已知：平行四边形两邻边长为a和b(a＜b)，两对角线的一个交角为θ(0°＜θ＜90°)，求该平行四边形的面积.

 

分析：由于已知了平行四边形相邻两边长和对角线的一个交角，再考虑到平行四边形的面积是△AOB的四倍，因此只要求OA·OB·sinθ即可.

解：设平行四边形ABCD的对角线AC与BD相交于O.AB=a,BC=b,∠AOB=θ，又设OA=x,OB=y.

在△AOB中，应用余弦定理可得：

a2=x2+y2-2xycosθ                ①

在△BOC中，应用余弦定理可得：

b2=x2+y2-2xycos(180°-θ)        ②

由②-①得：

b2-a2=4xycosθ

∵0°＜θ＜90°，∴xy= (b＞a)

∴S□=4S△AOB=2xysinθ=tanθ

例4  在△ABC中，已知4sinBsinC=1,b2+c2-a2=bc,且B＞C，求A、B、C.

分析：由于题设条件b2+c2-a2=bc十分特殊，将它与余弦定理对照可得A=60°,这样B+C=120°，于是再利用条件4sinBsinC=1，可求得B与C.

解：由余弦定理cosA===.

又∵0°＜A＜180°

∴A=60°

∴B+C=120°,又由于4sinBsinC=1

∴4sinBsin(120°-B)=1

∴4sinB(cosB+sinB)=1

∴sin2B+2sin2B=1

∴sin2B=cos2B

∴tan2B=,∴2B=30°或2B=210°

由于B+C=120°,且B＞C，60°＜B＜120°

∴2B=210°,

∴B=105°,从而C=15°

∴A=60°,B=105°,C=15°

例5  已知△ABC中，a，b，c为角A，B，C的对边，且a+c=2b，A-C=,求sinB的值.

解法一：由正弦定理和已知条件a+c=2b，得sinA+sinC=2sinB，由和差化积公式得

2sin·cos=2sinB

由A+B+C=π，得

sin=cos

又A-C=,得

cos=sinB

∴cos=2sin·cos

又∵0＜＜,cos≠0

∴sin=

从而cos==

∴sinB=· =.

解法二：由正弦定理和已知条件a+c=2b，得sinA+sinC=2sinB

∵A-C=,A+B+C=π

两式相减可得B=-2C

∴sin(+C)+sinC=2sinB

得sincosC+cossinC+sinC=2sinB

∴cosC+sinC=2sinB

即cos(-C)=2sinB

∴cos=4sin·cos

∵0＜B＜π,∴cos≠0

∴sin=

cos==

∴sinB=·cosB=

 

【难题巧解点拔】

例1  △ABC中，若a=5,b=4,cos(A-B)= ，求AB.

分析：很明显，只要求cosC的值，应用余弦定理即可求出AB.

解法一：由已知条件a=5,b=4

===9，①由已知cos(A-B)= ,根据半角公式有

sin==,cos==

代入①式得tg=  ∵tg=ctg,

∴tg= ,根据万能公式cosC=

∴c2=a2+b2-2abcosC=36,AB=c=6

解法二：∵A＞B，如图，作∠BAD=∠B,∴AD=BD

∠CAD=∠A-∠B令AD=BD=y,CD=x,

由余弦定理cos(A-B)== ,x=a-y,

∴= ,y=4,x=1

△CAD中再由余弦定理cosC=,∴c=6

评析：上述解法反映边向角的转化，也可由角向边转化直接求出边.

例2  半圆O的直径为2，A为直径延长线上的一点，且OA=2，B为半圆周上任意一点以AB为边向形外作等边三角形ABC(如图)，问B点在什么位置时，四边形OACB的面积最大，并求出这个最大面积.

解：设∠AOB=x，则

S△AOB=·2·1·sinx=sinx,

AB2=OA2+OB2-2·OA·OB·cosx=5-4cosx.

S△ABC=AB2= (5-4cosx)= -cosx

∴SOACB=S△AOB+S△ABC

=sinx-cosx+

=2sin(x-)+

∵0＜x＜π,- ＜x-＜  ∴x-=时，

∴即x=时,SOACB有最大值2+(平方单位)

例3  已知△ABC中，AB=AC=a,∠BAC=φ，等边三角形PQR的三边分别通过A，B，C三点.试求△PQR的面积的最大值.

分析：先依题意画出图形(如图).因为变动三角形PQR为正三角形，它的面积S=PQ2，问题可转化为求边长PQ的最大值.为此需要建立PQ的函数式，这又必须选取适当的量作为自变量.观察图形可以发现，PQ的位置是随着∠PAB的大小变化而变化的.不妨就以∠PAB为自变量.以下的程序就是应用三角形的边角关系，求出以∠PAB的三角函数表示PQ的解析式，最后求它的最大值.

解：设∠PAB=x,那么∠PBA=120°-x,∠QAC=180°-x-φ，∠QCA=x+φ-60°.

在△PAB中，∵=，

∴PA=sin(120°-x),

在△AQC中，=

∴AQ=sin(x+φ-60°)

∴PQ=PA+AQ=［sin(120°-x)+sin(x+φ-60°)］

=sin(+30°)cos(90°--x).

因为其中a, +30°都是常量，所以当90°--x=0即x=90°-时，取得

(PQ)max=sin(+30°)

同时也就取得了

(S△)max= (PQ)2max

=a2sin2(+30°)

例4  在△ABC中，已知A=，求证：＜c-a＜.

证明：在△ABC中，由A=，得C=2A，∴B=π-3A,∴0＜A＜

 ===

====.

∵0＜A＜，∴＜cosA＜1，即2＜2cosA+1＜3∴＜＜,故＜c-a＜.

评析：解本题的关键是利用正弦定理及三角公式将转化为，结合角A的取值范围推得结论.

 

【课本难题解答】

课本第132页，习题5.9第8题：

｜F｜≈132N，β≈38°

第9题

两条对角线的长分别是4cm和4cm,面积是48cm2.

 

【命题趋势分析】

本节主要考查：1.根据已知条件，求三角形的末知元素，或判断三角形的形状.

2.运用正、余弦定理及关系式A+B+C=π解决三角形中的计算和证明问题.

3.利用所学的三角知识解决与三角形有关的三角函数问题和简单的实际问题.

根据考试的方向，可以预见，利用正、余弦定理解斜三角形问题将会与三角函数、数列、方程、向量等知识相结合，尤其是与生活、生产、科学实验实际相结合，考查综合运用数学知识的能力.

 

【典型热点考题】

例1  在△ABC中，a，b，c分别是角A、B、C的对边，设a+c=2b，A-C=，求sinB的值.

解：根据正弦定理和已知可得：sinA+sinC=2sinB,A+B+C=π

则2sin·cos=2sinB.

又A-C=,sin=cos

∴2coscos=2sinB=4sincos

又∵0＜＜

∴sin=

cos== 

∴sinB=2··=

例2  若△ABC的三个内角A、B、C成等差数列，且最大边为最小边的2倍，则三内角之比为        .

解：设三角形三内角从小到大依次为B-d,B,B+d,

则B-d+B+B+d=180°∴B=60°

设最小边为x，则最大边为2x,

从而=tand=,d=30°

所以三内角分别为A=30°,B=60°,C=90°,得三内角之比为1∶2∶3.

∴应填1∶2∶3.

例3  在△ABC中，A、B、C三顶点所对边分别为a,b,c，试证明b2=c2+a2-2accosB.

证明：因为=+

则有：2=·=(+)·(+)

=2+2+2·

=2+2+2｜｜·｜｜cos(180°-B)

=c2+a2-2ac·cosB

所以b2=c2+a2-2ac·cosB

例4  求sin220°+cos280°+sin20cos80°的值.

解：设△ABC中的A=10°,B=20°,C=150°对应边分别为a,b,c.

△ABC的外接圆半径为2R，则由正弦定理得：

a=2Rsin10°,b=2Rsin20°,c=2Rsin150°

由余弦定理，得：

(2Rsin150°)2=(2Rsin10°)2+(2Rsin20°)2-2(2Rsin10°)(2Rsin20°)cos150°即：sin2150°=sin210°+sin220°+sin10°sin20°

则：cos280°+sin220°+sin20°cos80°=

说明：本题采用了构造法，题中余弦变正弦之后，注意到=-2cos(180°-10°-20°).